Valley Glaciers

Valley Glacier Dynamics and Structure

Hubbard, Bryn, Owain Bayley, David Chandler, Neil Glasser, Becky Goodsell and Michael J. Hambrey

Mer de Glace, France. The abandoned lateral moraine crest along the far margin clearly indicates the extent to which this typical Alpine glacier thinned through the 20th Century. Photo: B. Hubbard.

The recession of the Earth's smaller glaciers and ice caps has been responsible for ~50% of the 7 cm or so of sea-level rise recorded over the past century. These predominantly temperate glaciers are not only sensitive indicators of global change, but they are located in relatively heavily populated regions, presenting opportunities as resources and posing risks as hazards directly to local human populations. Since the Inter-governmental Panel on Climate Change anticipates continued anthropogenic warming well into the medium-term future, one of the principal challenges currently facing glaciologists is to predict the manner in which temperate ice masses will respond to this climate change. Our research in the Swiss and French Alps addresses this requirement, either directly, e.g. in terms of using field data to calibrate models of glacier response, or indirectly, e.g. in terms of our efforts to reconstruct the structure and flow mechanisms that characterize temperate Alpine glaciers.

Why is the study of temperate glaciers important?

Not only are results from temperate glaciers important from their own perspective, they are also important in studying the basic physical processes governing the behaviour of all ice masses. Most of the information presented below relating to research at dynamic Alpine glaciers is relevant to all ice masses, irrespective of ice-mass size or location. Indeed, the logistical simplicity of researching the behaviour of Alpine glaciers provides one of the most compelling reasons for carrying out such research. It is therefore not surprising that much of our most detailed knowledge relating to process glaciology relevant to all ice masses is provided by studies at smaller, temperate glaciers.

Using Field Data to Train and Calibrate Valley Glacier Models

Predictions of ice mass response to climate change are generally made by dynamic, spatially-distributed numerical models of ice-mass motion. At the core of these models is the ice flow equation, developed by John Glen in the 1950s, which is used to calculate the rate at which ice deforms under the stresses predicted by the model. As a result of recent mathematical and computational advances, these models can now be run in three dimensions, at high spatial resolution and to include longitudinal stress transfer along the glacier. They are therefore capable of generating sophisticated and precise stress fields. However, field glaciologists might well argue that such models are limited in their ability to calculate accurately how ice responds to stresses because natural ice masses are more complex than those models take them to be. This unaccounted-for complexity may be identified in three principal areas: (a) unaccounted-for spatial variations in ice softness; (b) unaccounted-for complexities in the physical structure and motion fields of ice masses; and (c) unaccounted-for basal motion by sliding and substrate deformation. Our research at the Centre for Glaciology has been designed to address all three these issues.

(a) Ice softness variations and glacier modelling

Field researchers have long realized that ice masses are characterized by a high degree of spatial variability in their physical composition. Each varying property exerts some control over ice softness, resulting in large-scale spatial variations in softness. Ice cores recovered from large polythermal ice masses for example indicate the presence of a basal ice layer, often of Pleistocene age, that is typically between three and 100 times softer than the overlying Holocene-age ice. This enhanced softness reflects variations in a suite of physical properties, although a preferred ice crystal orientation is central to most explanation. It is also probable that the liquid water content of ice (principally held within the inter-crystalline vein system) also plays an important role.

Despite this progress at large polythermal ice masses, models of valley glacier motion assume all temperate ice is of identical softness. This may be about to change. Importantly, results from ice coring in the Swiss Alps by staff at the Centre for Glaciology and colleagues clearly indicate that the physical structure of these temperate valley glaciers also varies systematically. Analysis of the crystallography, ionic composition, included debris and included gas of a series of ice cores from Tsanfleuron Glacier, Switzerland, led us and Belgian colleagues to argue for the presence of three distinctive zones at this temperate valley glacier. In this case, the Basal Zone (BZ) has a thickness of ~1.5 m above the ice-bed interface, the Lower Zone (LZ) extends for ~15 m above this, and the Upper Zone (UZ) extends from the top of the LZ to the glacier surface, as the following figure demonstrates.

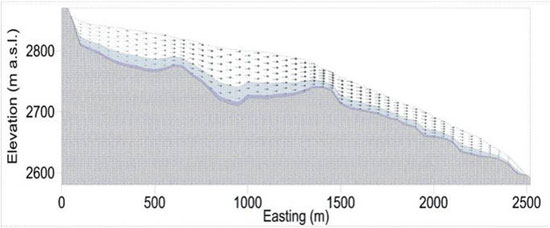
Schematic illustration in long section of the positioning of the three different ice types identified at Tsanfleuron Glacier, Switzerland. Here, the bedrock is grey and ice types are shaded in blue: from darker to lighter the BZ, the LZ and the UZ. (After Hubbard and others, 2003, Annals of Glaciology)

Following this, we (a) used measured bulk ionic concentrations of ice to approximate the water content and ice softness of each of the ice zones identified above; (b) incorporated those rheologies and their host zone geometries within a 2-d first-order flow model, and (c) ran the model for Tsanfleuron Glacier to compare the effects of the two physical configurations.

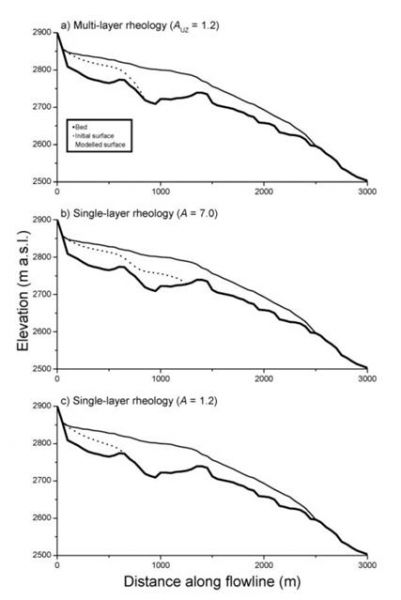
The resulting softnesses of LZ and BZ ice relative to that of UZ ice (termed AUZ) are respectively 1.80 (ALZ = 1.80 AUZ) and 10.74 (ABZ = 10.74 AUZ). To investigate the significance of these changes for model predictions results of the layered model were compared with those of a single-rheology (homogeneous) model run to steady-state under a simulated glacier retreat (from the 2001 geometry) in response to a 75 m step rise in the equilibrium line altitude. Results yield dramatically different predicted steady-state responses, illustrated in the figure above. While the layered model predicts a 78% reduction in area relative to that of 2001, the homogeneous model predicts a reduction of only 64%. Comparing these results reveals that the predicted homogeneous glacier is 65% larger than the predicted layered glacier.

(b) Structural glaciology and modelling

Models of ice flow assume conservation of momentum and spatial isotropy in the response of ice to stress (put another way: ice responds to similar stresses irrespective of the direction that stress is acting in). Thus, structural complexities such as brittle fractures and planes of preferential shearing are not catered for by any current model of ice-mass motion. However, all real glaciers are characterized by a degree of such complexity, and many are dominated by it. For example, surface and basal crevasse fields mark zones of brittle failure across which stresses are not propagated. Although very little is known about, for example, the integrity of ice at depth and zones of preferential motion, staff at the Centre for Glaciology have worked on reconstructing these phenomena at many different types of real ice masses. Indeed, Mike Hambrey's early research on the structural glaciology of Alpine glaciers such as Griesgletscher pointed to the complexities that in reality characterize even these relatively simple glaciers. Following this work, Mike, with former Cambridge colleagues Wendy Lawson and Martin Sharp, applied similar principles to his work as part of a team investigating the more complex structure of surge-type (and recently surged) Variegated Glacier, Alaska. Clearly, in situations such as these where the ice contains many structures of relative weakness the relationships between stress and strain become highly anisotropic.

More recently, staff at the Centre for Glaciology have been studying the relationships between the movement of polythermal glaciers, in particular those located in Svalbard, and the passage of debris through them. Although the primary focus of these studies was to identify the relationships between the sediment transport pathways through such glaciers, and the form of the resulting post-glacial deposits, an important by-product of the research has been the realization that even these geometrically-simple glaciers are actually structurally very complex. For example, our investigations of longitudinal ice-surface debris-charged ridges has led to the identification of glacier-wide transverse compression associated with ductile folding that is intense enough to bring debris from the glacier bed up to the surface. On the other hand, our investigations of the character of transverse surface debris ridges has led us to argue that they are formed by the brittle thrusting of basal ice through the body of the glacier to the ice surface. Both of these processes are illustrated in the figure below.

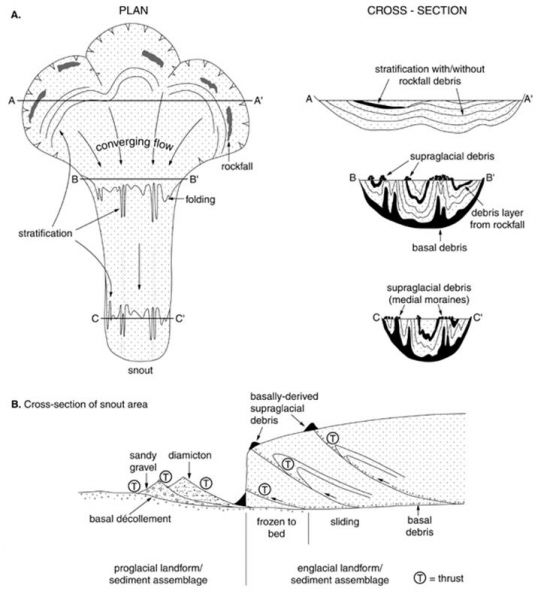
One further study, recently completed, is that of former postgraduate student Becky Goodsell (now a research fellow at the University of Canterbury, New Zealand). Becky studied the structural glaciology of Haut and Bas Glacier d'Arolla, Switzerland (photographs below). Again the investigation pointed to the presence of a wide range of structures, including stratification, folds, foliation, and crevasses in both glaciers. Further, the Bas Glacier is dominated by an icefall that produces a fine set of ogives (curving bands that extend across certain glaciers with icefalls), the origin of which has proved rather enigmatic to glaciologists. Becky has argued on the basis of her research that these features are physically complex and develop towards the base of icefalls where intense shear is responsible for propagating material from the glacier bed, allowing basal debris to reach the surface.

Clearly, the structure of real ice masses is more complex than current model formulation considers them to be. While we are still a long way from fully incorporating this information into models of ice mass motion, our work is beginning to point to the kinds of issues that need to be addressed.

(c) Basal motion

Periods of particularly fast ice motion, or steady speeds that exceed those caused by ice deformation alone, are generally caused by supplementary basal motion. At hard-bedded glaciers (i.e. those located on bedrock) this component is supplied by basal sliding. At soft-bedded glaciers (on soft sediments) the motion is more likely to be achieved by the deformation of those sediments. Since both these basal motion processes are strongly controlled by the presence and pressure of basal melt-water, models of ice mass motion generally lump both together into a single sliding term and invoke that term in all cells whose basal temperature attains the pressure melting point. For example, Payne and colleagues recently utilized a sliding term of the form:

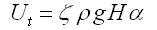
where Ut is the sliding velocity, ? is a constant ‘sliding parameter', ? is ice density, g is gravitational acceleration, H is local ice thickness and a is local ice surface slope. More recently though, Payne, in a newly-developed first-order thermo-mechanical model, allows ? to vary with the basal melt flux which goes some distance to incorporating variations in basal water pressure where there is a closed hydrological system under the assumption that subglacial water is immobile. This is typical of the state-of-the-art in numerical solutions to including sliding in large-scale models of ice mass motion.

Our borehole-based research at Haut Glacier d'Arolla has indicated that we may need to be more sophisticated in our approach to modelling ice masses - particularly where the effectiveness of different motion components depends on subglacial drainage. Initially, Harbor and colleagues noted that the major subglacial channel identified by us in 1995 that develops in a similar location each melt season acts as a corridor of low basal traction (termed a slippery zone). Annually repeated borehole inclinometry indicated that the classic cross-sectional velocity profile was severely disrupted above and near to this slippery zone (figure below).

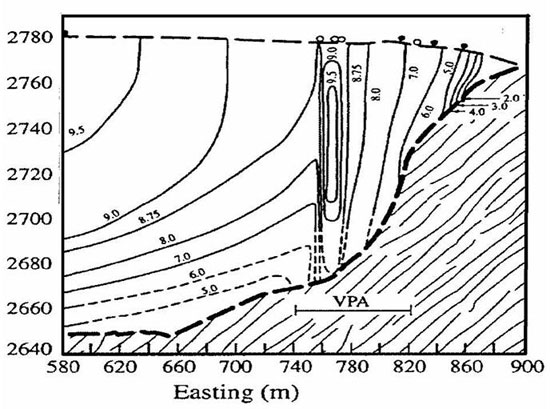
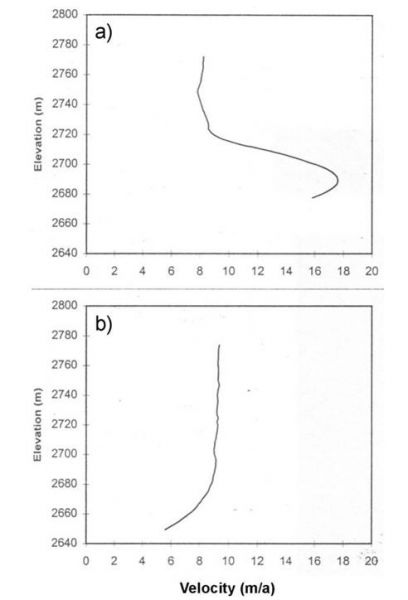
More recently, results from automated 3-d velocity measurements at the glacier obtained by Willis and colleagues, indicate that the slippery zone actually generates extrusion flow (Willis and others, 2003). In contrast, deformation profiles either side of the axis are characterized by standard power-functions (Figure below).

Our Alpine research also indicates that these spatial variations have a strong temporal dimension. Intra-annual velocities vary markedly, with dramatic speed-ups being recorded through the summer melt-season relative to the winter as noted by Willis. This summer speed up is caused by the onset of basal motion as large volumes of meltwater reach the glacier bed. Conversely, winter flow fields reflect motion by ice deformation alone. These allowed us to direct a 3-d, first-order algorithm in order to model the long-term aggregate pattern of down-glacier flow in this cross-section (Figure below). By perturbing the basal boundary condition and introducing a zone of reduced shear traction, we modelled the annually-averaged velocity as a composite, time-weighted average of 20 weeks 'winter' no sliding, 20 weeks 'normal summer' sliding and 12 weeks enhanced 'spring event' sliding and successfully replicated the extrusion flow observed over the preferential drainage axis. This success is noted both in terms of time (whereby the slippery zone develops during the spring event and the summer) and space (whereby the effects of the slippery zone expand as they are transferred upwards from the preferential drainage axis).

Finally, at the Centre for Glaciology we are working to identify precisely what basal sliding is. Theoretically, the process involves two distinct mechanisms: (a) enhanced ice deformation under very high and variable stresses close to the glacier bed, and (b) repeated melting-refreezing cycles around bedrock protrusions (termed regelation). However, how actual ice at the bed of the glacier moves over rough bedrock is not well understood. Through subglacial experimentation and instrumentation we have been able to measure basal sliding directly at several different glaciers. Initially, we measured sliding beneath the margin of Tsanfleuron Glacier in Switzerland, revealing a major pure slip component and systematic differences in the nature of individual motion events away from the ice-bed interface.

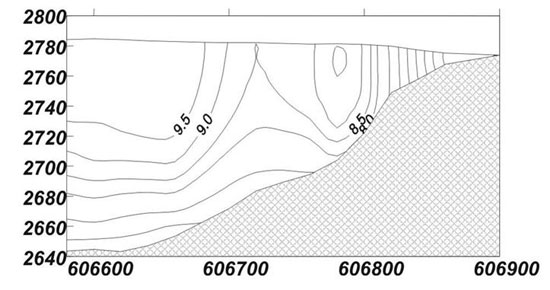
Velocity patterns (m/a) in the cross section at Haut Glacier d'Arolla predicted from a temporally distributed model of ice motion including a local basal sliding component for part of the year (After Hubbard and others, 1998, Journal of Glaciology)

Over the past two years, David Chandler has extended the study and techniques and applied them to numerous other field sites (including Greenland and New Zealand). Most notably, in 2003, David worked with scientists from University of Savoie and Emosson Power Company to measure sliding and seismicity deep beneath the ice fall of Argentière Glacier in France. Results of this study were published in 2004.